Статья «Стоит ли овчинка выделки…» собрала более 250 комментариев на портале e-xecutive.ru (на нашем сайте она находится здесь). Автор самой обсуждаемой публикации февраля 2016 года представляет теоретический подход к обоснованию своей формулы эффективности.
Обсуждение показало, что представленный материал вызвал больше новых вопросов, чем дал ответов. Выяснилось, например, что на данном этапе читателю нужна не формула эффективности, а скорее нужен ответ на вопрос: «Для чего нужна формула эффективности?» и «В чем сущность эффективности?».
Есть ли у меня понимание, что поднимая такую серьезную тему, я рискую попасть под несравнимо более мощный поток критики? Конечно, есть. Но, ведь исследователи проблемы поиска концептуального и количественного определения эффективности бизнеса, основываясь на использовании классических моделей и методов, так и не ответили на вопрос: «Что такое эффективность?».
Чем данная публикация может помочь специалистам в области управления? В первую очередь пониманием тех ограничений, которые накладывает на задачу, связанную с определением эффективности, использование того инструментария менеджера, который традиционно используется при попытке найти приемлемый ответ на эти вопросы. Ведь убежденность в том, что ты действительно выбираешь самый выгодный вариант инвестирования средств, не может опираться на тезис: если известная методика широко используется, она априори дает достоверные результаты.
Кому нужна определенность с понятием «эффективность»? Определенность нужна тому, кто хочет добиться максимальных темпов развития бизнеса. Если такой потребности нет, то нужно обратиться к теме экономии ресурсов.
1. В чем ограниченность рентабельности?
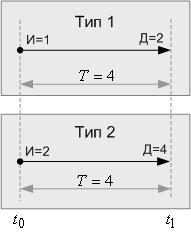
Чтобы разобраться с сущностью эффективности, лучше всего рассмотреть особенности ее проявления на конкретных примерах. Очевидно, что эффективность – относительный показатель. Чтобы убедиться в этом, рассмотрим два типа простых бизнес-операций (рисунок 1). Здесь И – инвестиции; Д – доход; Т – время операции.
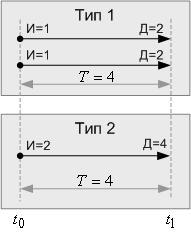
- Вывод 1. В случае равенства продолжительности двух простых операций (T1=T2) и равенства их рентабельности (R1=R2), эффективность исследуемых операций О1 и О2 эквивалентна, поскольку, для операции О1 с меньшими инвестициями всегда можно создать парную операцию О1.2 с дополнительными инвестициями О1.2=О2-О1, а результат проведения парных операций обеспечит получение равной суммарной прибыли, по отношению к операции О2.
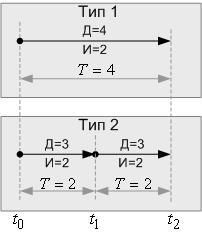
Этот факт, а также то, что показатель «рентабельность», в этом случае, дает правильный ответ на вопрос, связанный с оценкой эффективности, основываясь на базовых параметрах операции каждого типа, многими воспринимается как доказательство того, что рентабельность является синонимом эффективности. То, что это не так, показывает исследование двух типов операций с разной продолжительностью (рисунок 3).
Так, каждая из операций второго типа эффективней операции первого типа, хотя ее рентабельность в два раза ниже. Почему? Вложение инвестиций во второй тип операции позволяет в момент времени t1 вернуть их с прибылью в одну единицу и снова вложить полученные инвестиции в операцию с такими параметрами. В момент t2 снова вернуть вложенные инвестиции с прибылью в одну единицу.
Общая прибыль от вложения в операции первого типа к моменту t2 при этом составит две единицы. Такая же прибыль будет получена к моменту t2 и от операций второго типа.
Несмотря на то, что вложения и прямые доходы от процессов, построенных на операциях первого и второго типов равны, относительно эффективности эти операции не эквивалентны. Связано это с тем, что прибыль от операции второго типа, полученная в момент времени t1, сразу же может инвестироваться в новую операцию или проект.
Поскольку к моменту t2 вновь созданная операция с «родительской» рентабельностью принесет инвестору дополнительную прибыль, операция второго типа эффективнее операции первого типа. Продолжительность «дочерней» операции будет определяться уровнем спроса на ее потребительский продукт. В случае низкого спроса и необходимости «вписаться» в заданный интервал времени, новые инвестиции можно разбить на ряд более мелких по объему.
Вывод 2. Из двух типов простых операций с равными инвестициями (затратами) и кратным временем операций эффективней операция с меньшим временем, если на момент одновременного завершения процессов, построенных на этих типах операций, их процессуальная прибыль одинакова.
После анализа второго примера становится понятной сложность задачи, которую «должен решать» показатель эффективности. В частности, он должен указать, что операция второго типа (рисунок 3) эффективней операции первого типа, учитывая время этих операций, их рентабельность и эффект от инвестиции собственной прибыли.
Понятия «эффективность» и «эффективное использование ресурсов» в рамках данной работы — это синонимы. В свою очередь, чтобы дать определение понятию «эффективное использование ресурсов», а также вести предметный разговор в дальнейшем, необходимо создать базовый терминологический фундамент. Для получения общих выводов эта терминологическая база будет иметь кибернетическую направленность.
2. Система условных обозначений и целевая модель операции
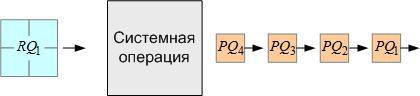
Условимся обозначать входные продукты операции базовыми символами R1, R2, R3…, а выходные продукты операции базовыми символами P1, P2, P3… (рисунок 4).
Для каждого значимого продукта операции должна быть получена экспертная оценка единицы продукта (стоимость единицы продукта). Для обозначения ценности единицы продукта к его базовому обозначению в нижнем регистре символов будем присоединять символ s. В этом случае экспертная оценка единицы входного продукта будет обозначаться для первого продукта rs1, а первого выходного продукта – ps1.
Символьные обозначения rs1 и ps1 строчные, потому что экспертная оценка – это параметр, который, в общем случае, изменяется во времени и не может быть проинтегрирован (также как, например, температура).
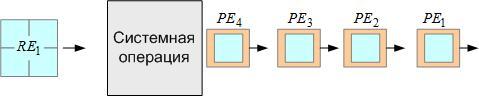
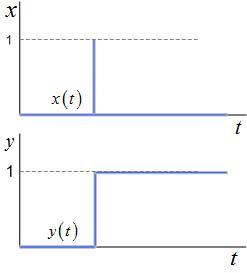
Экспертную оценку общего объема инвестиций будем обозначать присоединением символа E к базовым символам входных и выходных продуктов. Теперь, используя систему принятых обозначений, можно определить экспертную оценку первого входного и первого выходного продукта так RE1=rs1*RQ1 и PE1=ps1*PQ1 (рисунок 6).
Несколько сложнее с продуктами, параметры которых распределены во времени. Представьте, что мы рассматриваем операцию нагрева жидкости с использованием природного газа. Тогда мы можем говорить об общем количестве потребленного продукта, используя символьное обозначение RQg, когда говорим об объеме потребления, или REg, когда говорим об экспертной оценке или стоимости потребленного объема газа.
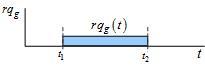
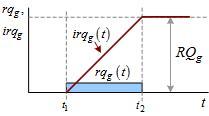
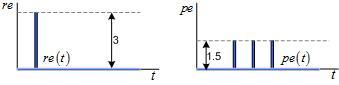
Если же нам нужна распределенная во времени модель продукта, а она нам понадобится, то мы будем переходить к системе с нижним регистром символов. Обозначение rqg(t) будет говорить о том, что, например, это расход газа Rg в единицу времени (рисунок 7).
Если необходимо определить объем потребляемого газа на интервале от t1 до t2, то он может быть получен из следующего выражения:
Чаще всего информация о системном процессе представлена в дискретном виде, в частности, в виде временных рядов. Интегрировать импульсные функции проще, чем непрерывные. Суть этого процесса отображена на рисунке 9, где x(t) — импульсная функция, а y(t), ее интеграл:
Модель с распределенными во времени выходными продуктами не очень удобна, как объект исследования. Поэтому упростим ее еще и введем понятие — «простая целевая операция».
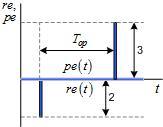
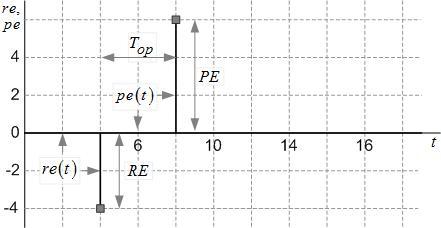
У такой модели есть только один входной продукт (инвестиции) с величиной экспертной оценки RE и один выходной продукт (целевой продукт – экономическая прибыль), с величиной экспертной оценки PE. Момент поступления продукта R на вход операции соответствует ее началу, а момент передачи выходного продукта P потребителю, моменту ее завершения. В таком случае любая простая целевая операция может быть описана тройкой параметров: RE, PE и Top (рисунки 11 и 12).
Какую модель лучше использовать, зависит от ситуации. Например, чтобы моделировать процесс, состоящий из нескольких целевых операций, понадобится векторная модель (рисунок 12). Для вывода формулы эффективности целевой операции, первая модель (рисунок 11).Каждый показатель тройки RE, PE и Top является одним из ее базовых параметров.
3. Понятие «системный эффект» — первый шаг к пониманию сущности эффективности
Определим систему базовых показателей простой целевой операции. Такими базовыми показателями будем считать показатели, которые получены на множестве базовых параметров, без использования каких-либо дополнительных преобразований модели простой операции.
К числу таких базовых показателей можно отнести:
- AE=PE-RE — добавленная ценность (добавленная стоимость, прибыль)
- kAE=(PE-RE)/RE — коэффициент добавленной ценности (рентабельность)
После завершения целевой операции, исследуемая система передает потребительский продукт с величиной экспертной оценки равной PE, системе потребления, в обмен на эквивалентный по ценности обменный продукт. При этом полученный обменный продукт представляет собой по сути две части ресурсов. Одна часть — эквивалент добавленной ценности (AE), вторая часть – эквивалент затратной части прошлой операции (RE).
Вопрос об эффективности использования ресурсов может подниматься только в том случае, если «бизнес-мышление» суперсистемы (владельца бизнеса) нацелено на максимизацию своих возможностей. В таком случае, например, процесс исследуемой системы непрерывен, а целевой продукт после его получения инвестируется во входной продукт новой системы, которая получив его, запускает параллельный системный процесс.
Если суперсистема выделяет часть своих ресурсов управляемой системе на выполнение одной операции, а по ее завершению забирает весь объем обменного продукта и останавливает процесс, и при этом у суперсистемы есть запас неиспользуемых ресурсов, то говорить об эффективном использовании ресурсов бессмысленно.
Как показывает история развития кибернетики и экономики, для которых эффективность является важнейшим показателем [БСЭ, т.29], разработать или вывести универсальный показатель эффективности с опорой на существующую теоретическую базу не удалось. Это означает, что решение этой задачи лежит за пределами существующих представлений о модели операции.
Ключом к решению этой задачи может оказаться, например, понятие «системный эффект» («экономический эффект»). То есть, «системный эффект» это, с одной стороны известное понятие, но понятие, оказавшееся золушкой в среде классиков экономической и кибернетической теорий.
В чем же уникальность понятия и сущности, определяемой как «эффект»? Если мы рассмотрим понятие «прибыль» и определим отношение этой категории к исследуемой операции, то заметим, что прибыль имеет прямое отношение к целевой операции, в рамках которой она была получена и определена. Совсем иное происходит с системным эффектом. Эффект не получают в рамках исследуемой операции и, соответственно не определяют в этих рамках. Эффект является результатом использования ресурса «прибыль», но в рамках другой системной операции.
Это первое. Вторая и более существенная ремарка, системный эффект – это не целевой продукт. Это процесс во времени. Таким образом, чтобы определить эффективность, нужно установить отношение между процессами в прошлом и будущем.
Но задача исследуемой операции — это «забота» о своей собственной эффективности, а не об эффективности какой-то будущей операции. Поэтому устанавливать отношение нужно между потенциальным эффектом будущего и процессами использования ресурсов в прошлом. Размышляя таким образом, можно представить показатель эффективности в общем виде, как отношение потенциального эффекта от использования прибыли в будущем, к показателю, характеризующему использование ресурсов в рамках исследуемой операции E= A/RES.
Опираясь на формулу эффективности в общем виде, можно дать определение понятию эффективности. Для этого определим абсолютный показатель RES, характеризующий связанные ресурсы исследуемой операции, как ресурсоемкость операции.
- Определение. Эффективность целевой операции определяется отношением абсолютного потенциального эффекта, который будет получен от инвестиции полученного целевого продукта в рамках исследуемой целевой операции, к ресурсоемкости исследуемой целевой операции.
4. Ключ к получению формулы эффективности — развернутая модель целевой операции
Чтобы попытаться вывести формулу ресурсоемкости RES, необходимо построить модель целевой операции нового класса. Давайте определим, в чем особенность моделей этого нового класса.
Как было отмечено, системный эффект проявляется в процессе освоения инвестиций. А построенная ранее модель целевой операции отображает не процесс во времени, а «снимки» процесса в момент регистрации входных и выходных продуктов (рисунок 13).
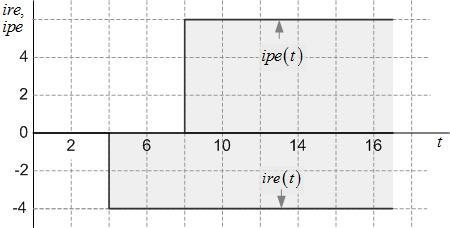
Чтобы модель операции реально отображала динамику процессов, необходимо на основании «снимков» восстановить картину движения продуктов в рамках исследуемой операции. Чтобы преобразовать «снимок» регистрационной модели операции в картину, прорисовывающую процесс движения входного и выходного продукта, необходимо проинтегрировать функции re(t) и pe(t). В результате мы получим развернутую модель простой целевой операции в виде функций ire(t) и ipe(t), показанную на рисунке 14.
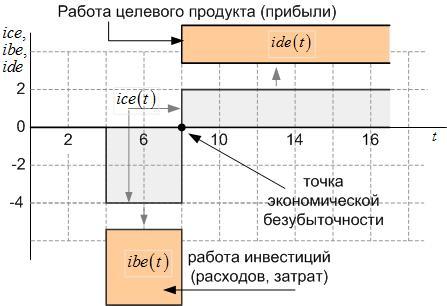
Если построить разность этих функций, то получим динамическую модель простой целевой операции в виде одной функции ice(t). В свою очередь, функцию ice(t) можно представить в виде двух функций: функции ibe(t) и ide(t) — см. рисунок 15.
Закрытый поток ibe(t) представляет собой работу инвестиций в исследуемой операции, а открытый поток ide(t) — работу целевого продукта в новой операции.
5. Комплексная рентабельность — почти «формула эффективности» для моделей простых целевых операций
Выскажем гипотезу, что работа целевого продукта на единичном интервале с момента завершения целевой операции — это потенциальный эффект. Его величина AET определяется площадью прямоугольника из соотношения AET=(PE-RE)xT1. Следовательно, можно предположить, что отношение площади AET к площади RET=RExTop и является показателем эффективности (EТ), который можно использовать в качестве критерия эффективности. Тогда EТ=АЕТ/RET. Определим полученный показатель понятием «комплексная рентабельность».
Рассмотрим три пары операций, эффективность которых можно определить, используя логический подход.
| № | И1 | Д1 | Т1 | И2 | Д2 | Т2 | Е | ЕT1 | ЕT2 |
| 1 | 2 | 3 | 2 | 2 | 4 | 2 | Е1<Е2 | 0.25 | 0.5 |
| 2 | 2 | 3 | 2 | 2 | 3 | 3 | Е1>Е2 | 0.25 | 0.1667 |
| 3 | 2 | 3 | 2 | 3 | 4 | 2 | Е1>Е2 | 0.25 | 0.1667 |
Таблица 1
Анализ показывает, что полученный показатель комплексной рентабельности (ЕТ) справился с поставленными ему задачами. Что же получается? Задача решена, и разработанный показатель успешно решает проблему оценки эффективности, по крайней мере, простых целевых операций?
Здесь очень легко можно сделать ошибочное предположение о том, что показатель ЕT является индикатором эффективности для всего класса простых целевых операций. Чтобы доказать его неспособность количественно сравнивать эффективность разных классов простых целевых операций, достаточно оценить эффективность операций (рисунок 3).
Как было определено ранее, Е1>Е2. Вычисления показывают, что ЕТ1=ЕТ2. Это означает, что критерий комплексной рентабельности не является критерием эффективности, показатель АET не является потенциальным эффектом, а показатель RET не является ресурсоемкостью.
Является ли полученный результат бесполезным с практической точки зрения? Очевидно, что нет. Показатель ET дает возможность использовать один универсальный тестовый инструмент, для сравнительной оценки эффективности простых целевых операций в рамках одного узкого класса. Что он дает с научной точки зрения? С научной точки зрения полученный результат показывает потенциал развернутой (динамической) модели целевой операции.
6. Как определить реальную точку безубыточности целевой операции?
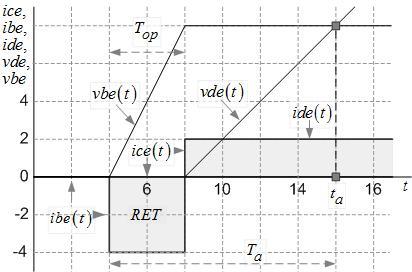
В экономике есть понятие точки безубыточности. Используя принятую систему условных обозначений, такую точку можно определить как точку пересечения оси времени функцией ice(t), как показано на рисунке 17. Но методика определения экономической точки безубыточности страдает существенным изъяном. Она не чувствует всех тонкостей, связанных с потерями исследуемого процесса.
Давайте рассмотрим логику отношений процесса ресурсопотребления исследуемой операции и процесса ресурсоотдачи от использования ее целевого продукта, как результата новых инвестиций.
Закрытый поток ресурсопотребления ibe(t) зависит от двух параметров. Это объем инвестиций и время их связанного состояния. Когда же работа целевого продукта (прибыли), компенсирует эту комплексную затратную часть? Учитывая, что мы рассматриваем модель простой целевой операции, ответ легко можно получить, используя координатную сетку. Количество прямоугольников внутри сетки равно четырем. Следовательно, момент компенсации потока ресурсопотребления потоком ресурсоотдачи будет находиться в точке ta.
В общем случае положение этой точки на временной оси можно определить графически как точку пересечений функций vbe(t) и vde(t), как показано на рисунке 16.
О чем говорит новая точка безубыточности? Она говорит о том, что для получения нового класса показателей целевых операций, в том числе формулы эффективности, нужно исследовать модель целевой операции не на интервале Top, а в рамках интервала Ta. Формула, представленная в прошлой статье «Стоит ли овчинка выделки: как математически оценить эффективность», назовем ее формулой EFFLI, была получена в результате исследования именно динамической модели целевой операции.
Показатель рентабельность был получен с использованием данных учетной модели операции (рис.13). Разные «родители», разные показатели, разная область применения.
Вот почему рентабельность — это не эффективность.



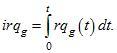
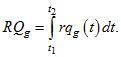
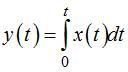



Оставить комментарий