Думаем, что читателям будет интересно познакомиться со статьей профессора механико-математического факультета МГУ Алексея Ивановича Чуличкова из «Науки и жизни«.
МАЛЫЕ ПАРАМЕТРЫ БОЛЬШИХ КАТАСТРОФ
Мы привыкли к стабильности и постоянству. Мы ступаем по твердой поверхности Земли и верим, что она всегда будет служить нам опорой. Мы знаем, что вслед за зимой придет лето, станет тепло и солнечно, и так будет всегда. Мы думаем, что мир вокруг нас не может внезапно измениться, и, исходя из этого, формируем свой образ жизни и приоритеты, планируем свои действия.
Такая привычная, «бытовая» точка зрения на устойчивость нашего мира нашла свое отражение в науке XVIII века, когда создавалось классическое естествознание. Его основой стал математический язык дифференциального и интегрального исчислений; считалось, что все зависимости можно описывать непрерывными функциями, для которых характерно небольшое изменение значения функции при малых приращениях аргументов. Казалось бы, логично: приложено чуть больше усилий — получен чуть больший результат… Более того, если математические модели не отвечали этим условиям, то они считались некорректными, а значит, лишенными реального содержания.
Но… Легкий поворот выключателя приводит в действие управляющие механизмы, и открываются створки плотины, мощные потоки воды обрушиваются на лопатки турбин, заставляя крутиться многотонный вал генератора. Легкий удар по детонатору вызывает взрыв, при котором мгновенно высвобождается энергия, сравнимая с энергией маленького солнца. Есть примеры и нерукотворных природных процессов, когда в результате слабого воздействия пробуждаются силы, во много раз более мощные: маленький камешек может вызвать горный обвал, страшную по своим последствиям снежную лавину и даже землетрясение. Научная и инженерная мысль открыла множество примеров скачкообразного изменения системы при малых воздействиях, но, как ни странно, на наши представления об окружающем мире до недавнего времени это почти не влияло.
Еще в древности, например в античной Греции, среди философов существовало представление, что вся природа живет и развивается благодаря соразмерности и гармонии величайших сил — противоположностей, находящихся в равновесии. Нарушение этого равновесия может разрушить весь мир. За гармонию противоположностей отвечают боги, и они прикладывают немалые усилия для ее сохранения. Вспомним миф о Фаэтоне, который упросил своего отца Гелиоса дать ему небесную колесницу в доказательство его божественного происхождения. Руки смертного не удержали небесных коней, он не сумел провести колесницу по безопасному пути, где солнечные лучи не опаляют землю, но и не дают ей замерзнуть. Последствия не заставили себя ждать:
Трещины почва дала, и в Тартар
проник через щели
Свет, и подземных царя с супругою
в ужас приводит.
Море сжимается.
Вот уж песчаная ныне равнина,
Где было море вчера;
покрытые раньше водою
Горы встают…
Овидий. Метаморфозы.
Чтобы вернуть мир из хаоса, потребовалось вмешательство верховного божества Зевса, восстановившего порядок.
Древние философы понимали, что даже малые изменения, нарушающие гармонию, могут существенно изменить мир, ввергнуть его в хаос. Многие столетия их внимание занимали именно законы этой гармонии, ибо в ней они видели проявление божественной воли, удерживающей мир в порядке. Начиная с пифагорейцев, открывших, что эти законы могут быть записаны на языке цифр и геометрических фигур, математику стали использовать как средство отражения идеальных законов природы, в которой все противоположности соразмерны и уравновешены. Может быть, этим и объясняется упорное нежелание «классических» математиков рассматривать неустойчивые математические модели, в которых возможно резкое нарушение равновесия.
Лишь в ХХ веке появились работы, в которых всерьез заговорили о том, что такие неустойчивости столь же реальны, как и состояния гармонии. Было осознано, что любая система, развиваясь, проходит этапы перестройки, резкого изменения, во время которых происходит перегруппировка сил, переустройство равновесия. Эти этапы характеризуются временным преобладанием одной из сил, что приводит к хаосу, разрушающему предыдущие структуры; затем происходит гармонизация, равновесие восстанавливается, но уже в новом, качественно ином состоянии.
Одной из математических теорий, описывающих резкие переходы, является теория катастроф. Как научная дисциплина она появилась в 70-х годах прошедшего века. Важным достоинством этой теории является то, что она не требует подробных математических моделей и может описывать ситуации не «количественно», а «качественно», а ее результаты и выводы иллюстрируются простыми геометрическими образами.
Такая «наглядность» теории катастроф привела к бурному росту числа публикаций, и наряду с серьезными работами, посвященными, например, устойчивости кораблей, описанию психических явлений, социальных и экономических процессов, появились работы полушутливого характера. Ниже мы приведем один из примеров такого «спекулятивного» использования метода теории катастроф, наглядно поясняющий ее суть. Но прежде объясним, насколько это возможно, на каких представлениях основана эта теория.
Положим, вам нужно описать зависимость некоторой величины x от двух параметров — m1 и m2. Для этого удобно использовать график этой зависимости, который изображается некоторой поверхностью, «висящей» над плоскостью параметров: два числовых значения параметров задают точку на плоскости, а высота поверхности над этой точкой дает значение исследуемой величины. Поверхность, из общих соображений и в соответствии с классическими положениями, будем считать «гладкой»; ее можно представить как лист бумаги, свернутый без разрезов и разрывов (рис. 1).
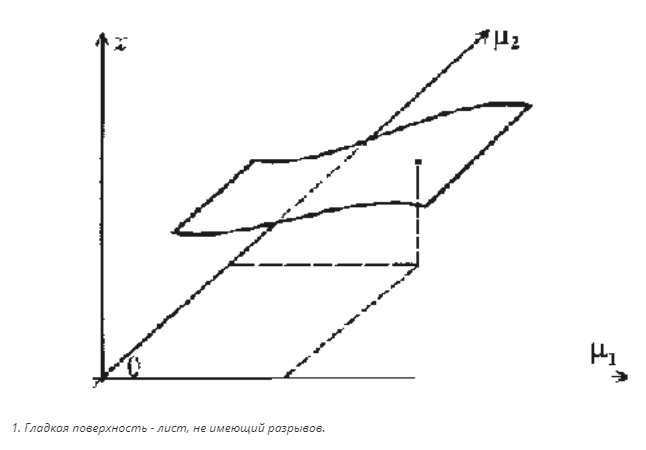
Зависимость не будет иметь особенностей, если каждому значению параметров соответствует только одна точка поверхности, — это случай, когда наш лист бумаги не имеет складок. Если же складки имеются, то возможны особенности двух типов. Одна из них так и называется «складка», она изображена на рис. 2.
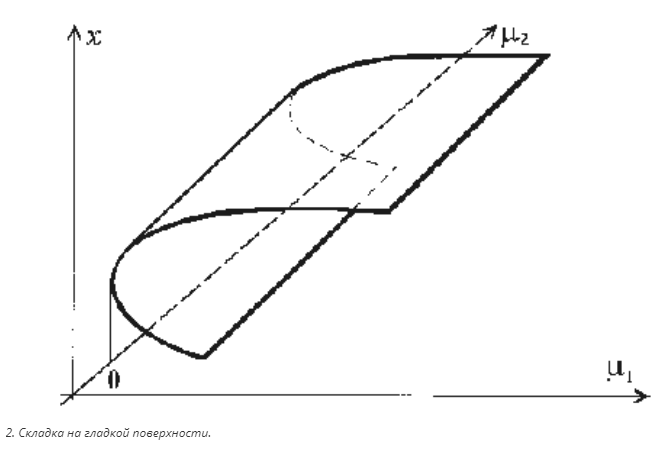
А другая получается, когда в одной точке (на плоскости параметров) встречаются две складки поверхности. Она носит название «сборка» и изображена на рис. 3. Проекция сборки на плоскость параметров обозначена буквой B.
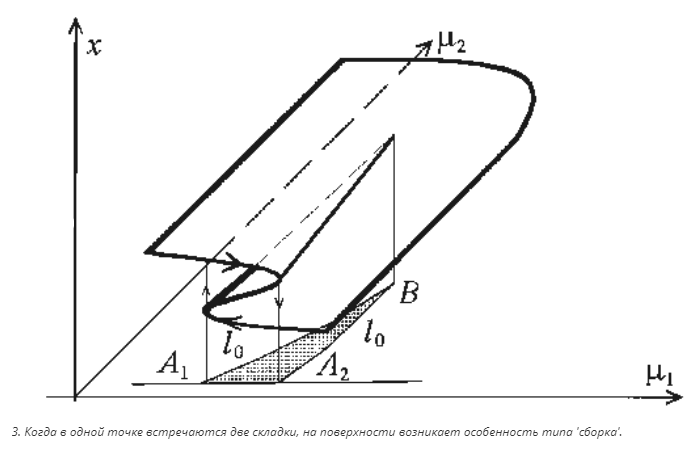
Подчеркнем, что, кроме указанных особенностей, никаких других в принципе быть не может — все остальные могут лишь комбинироваться из этих простейших элементов. «Катастрофа», то есть резкое изменение значения величины x, происходит, например, когда изменяется параметр m1 вдоль прямой A1— A2. Однако иное качественное поведение можно получить при изменении параметров в окрестности точки B.
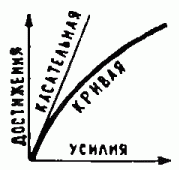
Вернемся к обещанному примеру. Он принадлежит английскому математику К. Зиману и приведен в замечательной популярной книге В. Арнольда «Теория катастроф». Речь идет об описании творческого процесса ученого, и величина Д характеризует его достижения в зависимости от увлеченности (параметр У на рис. 4) и владения техникой и навыками исследователя (параметр Т).
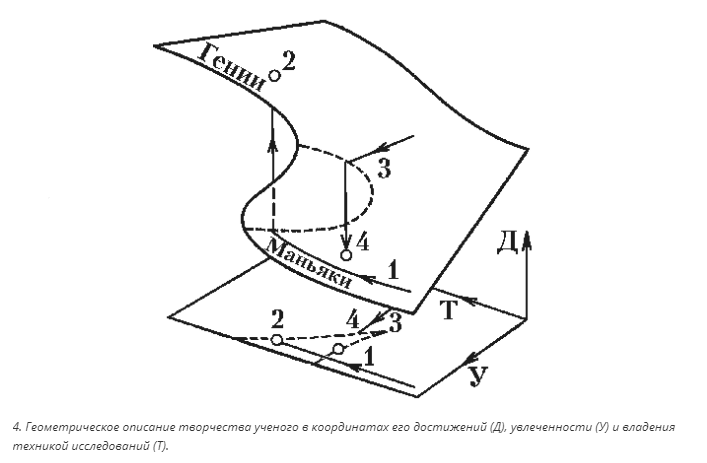
Если увлеченность невелика, то достижения вяло и монотонно увеличиваются с ростом профессиональных навыков. Если же увлеченность высока, то наступают качественно новые явления: с ростом профессионализма достижения могут возрастать скачком. Такая «катастрофа» вполне желанна. Область высоких достижений в этом случае можно назвать словом «гении». На рис. 4 данная ситуация соответствует движению из точки 1 к точке 2.
Если же рост увлеченности не подкреплен соответствующим ростом профессионализма, то происходит катастрофа в полном смысле этого слова: достижения скачком падают, и мы попадаем в область, обозначенную словом «маньяки» (это происходит при движении из точки 3 в точку 4 на рис. 4). Интересно, что скачки из состояния «гении» в состояние «маньяки» происходят на разных линиях, и при достаточно большом значении увлеченности гений и маньяк при равной технике и увлеченности различаются лишь уровнем достижений.
Заметим, что скачок достижений (рис. 3) происходит при разных значениях параметров в зависимости от того, движемся ли мы слева направо или справа налево вдоль прямой A1— A2. Это так называемая петля гистерезиса, демонстрирующая, что если вы из-за потери увлеченности потерпели катастрофу в уровне достижений, то для того, чтобы вернуть их на прежний уровень, необходима значительно большая увлеченность, чем та, что имелась накануне скачка.
Несмотря на всю привлекательность и интуитивную ясность подобных рассуждений, профессиональные математики весьма скептически относятся к обоснованности построений такого рода. Однако есть и более строгие результаты, касающиеся, например, математических проблем устойчивости развивающихся во времени процессов.
Теория катастроф на качественном уровне объясняет множество явлений. Вот, например, как можно пояснить возможность резкого изменения экологической обстановки на нашей планете. Для простоты введем некоторый обобщенный параметр x, характеризующий качество рассматриваемой ситуации с экологической точки зрения, например среднее содержание вредных примесей в атмосфере. Пусть реализуемы только такие значения x, при которых некоторая функция принимает свое минимальное значение — по аналогии с механикой, где все тела стремятся к минимуму потенциальной энергии. Следуя аналогии, назовем эту функцию «потенциалом». Ее график изображен на рис. 5.
Пусть при некоторых условиях зависимость потенциала от x изображается графиком на рис. 5а (условия, определяющие характер этой зависимости, остаются «за кадром»). Малые возмущения системы, обусловленные, например, деятельностью человека, могут лишь немного изменять загрязненность атмосферы — устойчивое состояние находится в одной из точек локального минимума в нижней части графика на рис. 5а (система «сидит» в этой точке надежно, как тяжелый шарик, скатившийся на дно лунки). Перевод системы в опасное состояние — в соседний локальный минимум, соответствующий высокой загрязненности, — практически невозможен: нужен слишком большой толчок, заставляющий систему (в нашей аналогии — тяжелый шарик) преодолеть высокий барьер, отделяющий точки минимума.
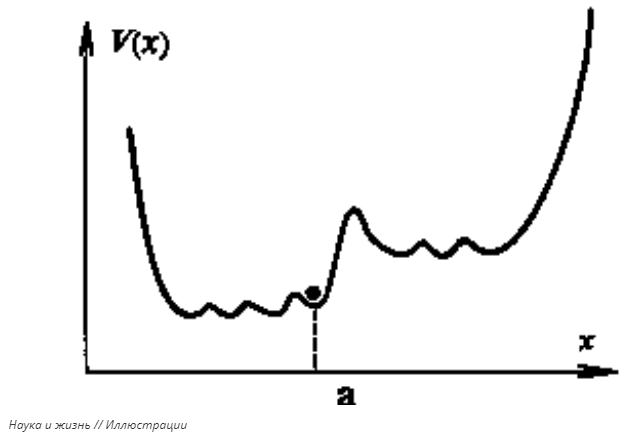
Однако при изменении условий (например, при накоплении отходов промышленного производства) характер зависимости потенциала от x может измениться и принять вид, изображенный на рис. 5б. Тогда даже небольшой толчок может заставить систему «свалиться» в устойчивое состояние с высоким уровнем загрязненности атмосферы. Такой переход может совершиться очень быстро, в считанные годы.

Рене Том
Теория катастроф, наряду с другими современными теориями динамических систем, уже в значительной степени изменила привычные представления об устойчивости и инерционности мира. Благодаря ей мы сегодня (хочется надеяться) лучше понимаем свою ответственность за возможные нарушения гармонии и равновесия противоположных природных сил, к которым ведет неограниченный рост промышленного производства в обществе потребления. Сейчас раздается все больше голосов за то, чтобы провести переоценку ценностей в современном мире и вслед за мудрецами древности вновь начать ценить красоту и соразмерность выше материального изобилия. Ведь если этого не произойдет, то поистине пророческими могут стать слова творца теории катастроф французского ученого Рене Тома: «Быть может, удастся доказать неизбежность некоторых катастроф, например болезней или смерти. Познание не обязательно будет обещанием успеха или выживания: оно может вести также к уверенности в нашем поражении, в нашем конце».
Но наряду со столь мрачными перспективами эта теория открывает и другие возможности. Действительно, коль скоро мы уверились в том, что при определенных условиях очень малые воздействия могут привести к значимым результатам, есть резон не опускать руки даже в самых тупиковых ситуациях — ведь, может быть, кажущаяся безысходность есть лишь признак надвигающейся «катастрофы», обещающей нам новый период расцвета.
История дает немало примеров, когда в критические моменты судьбы народов зависели от решения одного человека, и если ему удавалось «поймать момент», понять необходимость того или иного действия, то начиналось новое время, открывались новые перспективы, воплощались великие идеи. Так, Перикл, обратившись к идеалам единства и гармонии, после страшных разрушений греко-персидских войн привел Аттику к золотому веку классики, когда создавались совершенные вещи — скульптуры, храмы, научные и философские концепции, — к которым мы и сегодня обращаемся как к эталону. При Перикле творили великие Фидий, Анаксагор, Геродот; при нем заново отстроили Акрополь, ставший образцом прекрасного на многие века. Так же девятнадцать веков спустя Козимо Медичи, поддержав возникший интерес к античной культуре, положил начало Ренессансу — эпохе, перевернув шей жизнь средневековой Европы.
Поскольку в определенных ситуациях — в точках катастроф — даже незначительные движения могут повлиять на ход развития, очень полезным окажется умение определять, далеко ли от такой точки находится система. Формально для этого следует изучить зависимость системы от внешних параметров в математических моделях, однако на практике нередко встречаются случаи, когда у исследователя нет даже туманных соображений о том, каким эволюционным уравнением описывается развитие системы. Тем не менее даже в этих ситуациях, патологических с точки зрения математического моделирования, можно указать некоторые косвенные признаки того, что изучаемая система находится вблизи точки катастрофы.
Речь идет о так называемых «флагах катастроф» — особенностях поведения системы, по которым можно судить о приближении критической точки. Перечислим некоторые из них, чаще всего встречающиеся вместе:
- наличие нескольких различных (устойчивых) состояний;
- существование неустойчивых состояний, из которых система выводится слабыми «толчками»;
- возможность быстрого изменения системы при малых изменениях внешних условий;
- необратимость системы (невозможность вернуться к прежним условиям);
- гистерезис, который мы уже рассматривали в примере с «гениями» и «маньяками».
Чтобы проиллюстрировать эти ситуации, можно привести множество примеров из физики, но обратимся лучше к примерам более «жизненным».
Всем нам после окончания средней школы приходилось выбирать дальнейший жизненный путь. Первый «флаг катастрофы» — существование различных устойчивых состояний — проявляется в том, что мы можем видеть несколько различных привлекательных для нас вариантов деятельности. Это могут быть несколько институтов, в которые мы можем поступить (в последние годы благодаря вступительным олимпиадам школьник к моменту окончания школы может быть уже зачислен в несколько вузов), несколько фирм, где нас согласны принять на работу, и т. п. Наряду с этим присутствует и второй «флаг» — неустойчивые состояния — места, где мы уж точно надолго не задержимся. Третий «флаг»: приняв решение и став, например, студентом, мы испытываем стремительное изменение — и внешнее (меняется наш социальный статус, у нас появляются собственные деньги, пусть небольшие), и внутреннее (мы стремительно взрослеем). Четвертый «флаг»: после выбора обратный путь практически невозможен — чтобы нас отчислили с первого курса, еще до сессии, нужно натворить что-то очень грандиозное. Но уж если отчислили, то просто так обратно не примут, и надо ждать подходящих условий — новых приемных экзаменов. Это пятый «флаг катастрофы».
Еще одним «флагом катастрофы» служит так называемое «критическое замедление», когда множество усилий не приводит к сколько-нибудь заметному изменению ситуации. Такой флаг был вывешен на историческом пути нашей страны в 80-е годы, когда колоссальные средства, вкладываемые в экономику, например в сельское хозяйство, уходили словно в песок, ничего существенно не изменяя.
Нетрудно заметить, что если исследователь наткнулся на один из этих «флагов», то управляющие параметры можно поменять так, чтобы стало возможным обнаружить и другие «флаги», которые обязательно должны проявить себя в подходящих условиях. Правда, в рассмотренном нами примере с выбором института экспериментировать вовсе не обязательно и даже нежелательно, если только вы не хотите пожертвовать собой ради подтверждения теории. Но в иных условиях, чтобы убедиться, что система действительно может претерпеть резкий скачок состояния, имеет смысл поискать и более представительный набор «флагов катастроф».
ПРЕДОПРЕДЕЛЕННОСТЬ ИЛИ СВОБОДА ВЫБОРА?
Теория катастроф является одной из частей более общей математической теории — качественной теории сложных нелинейных систем. Эта теория изучает общие принципы, проявляющиеся в различных ситуациях, и помогает лучше понять механизм действия природных сил. Один из таких механизмов описывает взаимодействие судьбы и свободы выбора, и математическая модель этого взаимодействия оказывается очень близка к мифологической.
В религиозных и философских системах судьба человека связывается с его предназначением, с его жизненным путем, определенным свыше. В мифах античности судьбой человека распоряжаются дочери Зевса Мойры, непреодолимость рока символизируется водами подземной реки Стикс. Если механизм рока запущен, то любое поведение героя неотвратимо влечет его к развязке (как, например, в ситуации с Эдипом, которому было предсказано убить своего отца), однако всегда существует один-единственный поступок, казалось бы, незначительный в сравнении с масштабом последующих событий, который запускает их череду; герой мог бы поступить иначе, и тогда мифическая история пошла бы совсем по другому пути. Примером этому может служить решение Париса отдать яблоко Афродите, что вызывает целый ряд неотвратимых последствий, вплоть до Троянской войны и путешествия Одиссея.
Суд Париса
Вопросы о том, что определяет развитие мира, волновали умы мудрецов еще с древних времен. Анаксимандр из Милета (610- 540 до н. э.) учил: «Природа вечна, но в своем развитии она проходит через определенные фазы». Гераклит из Эфеса (520- 460 до н. э.) утверждал, что мир есть вечно существующий живой огонь, мерно разгорающийся и мерно потухающий. Следуя им, Эмпедокл из Акраганта (490- 430 до н.э.) считал, что мир проходит через бесконечную череду этапов — время господства «любви» сменяется периодом господства «вражды» и т. д. Основная идея античной философии: мир существует вечно, и сегодняшнее его состояние — лишь одна из многих ступеней его пути. Однако единая основа мира неподвижна — об этом говорили и Платон, и философы-элеаты. Идея о том, что вселенной управляют математические законы, традиционно приписывается Пифагору. Он учил: «все есть число» и «числа правят миром». Все явления мира гармоничны, а законы гармонии задаются отношениями целых чисел, как частоты нот в консонансном аккорде.
Итак, гармония вечна и неизменна. Судьба же — это движение, она определяет наше будущее, неизвестное сейчас. Математические принципы развития появились значительно позже, в конце XVII века, с развитием исчислений бесконечно малых: описав взаимодей ствие частей системы и ее начальное состояние, можно было однозначно определить ее эволюцию. Казалось, тайна вселенной раскрыта — ее будущее уже определено настоящим, все предрешено, и все можно предсказать, решив дифференциальное уравнение, хотя и очень сложное.
Выразителем этой крайней точки зрения считают Бенедикта Спинозу (1632- 1677): он утверждал, что в природе вещей нет ничего случайного, существует только необходимость, обусловленная законами природы. Случайность же приходится привлекать там, где мы чего-то не знаем.
В XVII- XIX веках этой детерминистской точки зрения придерживались большинство ученых. Предопределенность была синонимом объективности научных знаний, возможность точных предсказаний рассматривалась как величайший триумф науки.
Но трудно поверить в то, что миллионы лет назад уже были точно запрограммированы и появление жизни, и все катаклизмы и войны, и все радости и напасти рода человеческого, и все наши поступки, порой такие непредсказуемые и неожиданные. Возможно ли такое?
Наука ХХ века дала множество математических моделей, которые свидетельствуют, что в специально организованной среде действительно могут возникать новые формы, не существовавшие ранее. Одна из них была предложена Дж. Конвеем как забавное развлечение, но из-за множества аналогий вдруг приобрела глубокий смысл. Речь идет об игре «Жизнь». (Подробное описание этой игры под названием «Эволюция» см. в журнале «Наука и жизнь» № 8, 1971 г.; № 8, 1972 г. — Прим. ред.)
От авторов сайта: онлайн-вариант игры можно посмотреть здесь.
Правила ее очень просты: на тетрадном листе бумаги в ячейках прямоугольной сетки «живут» клеточки, подчиняясь простым правилам: если число соседей клетки больше трех или меньше двух, то она умирает. В пустой же ячейке с тремя «живыми» соседями может родиться новая клетка. Колония клеток демонстрирует разнообразное поведение в зависимости от начального состояния. Некоторые структуры исчезают, другие достигают стационарного поведения. Есть сообщества клеток, которые движутся, словно живые, — к ним относится так называемый «планер», или «парусник». Есть и более сложные конфигурации, например «планерное ружье», — эта колония клеток через 30 поколений возвращается в исходное состояние, рождая при этом один планер. Есть и «пожиратель планеров» — конструкция, которая поглощает налетающий на нее парусник и вновь поджидает очередную жертву.
Еще один пример. Простейшие математические формулы, определяющие расположение точек на плоскости, порождают необычайно сложные по своей структуре геометрические объекты — фракталы (см. «Наука и жизнь» № 4, 1994 г.). Их узоры складываются из бесконечных повторений и вариаций фрагментов. Колоссальное разнообразие этих форм достигается изменением параметров в математическом законе их построения.
Эти примеры свидетельствуют о том, что в самой природе среды, в ее структуре может быть заложена возможность творить невероятное количество форм. Среда, словно первобытный хаос, наделена множеством структур. Проявить то или иное потенциальное состояние среды можно, определенным образом организовав ее начальную структуру: расставив живые клеточки, «зерна» жизни в первом примере или задав параметры закона повторения фрагментов в примере с фракталами.
Казалось бы, тезис Спинозы подтверждается, и мы — люди, привыкшие считать себя свободными в выборе своего жизненного пути, — тем не менее действуем в соответствии с неумолимыми законами судьбы, предписанными нашим окружением. И все наши мысли, стремления, эмоции, вдохновения и открытия оказываются следствием изначального распределения частичек вселенной…
Но рассмотрим еще один пример — игру в бильярд. Начальная пирамида разбивается первым шаром — порядок сменяется хаосом. Если толкнуть все шарики так, чтобы они покатились в обратном направлении, приобретя те же скорости, то, как предписывают математические законы движения, все они из хаоса соберутся в первоначальную пирамидку. Однако попытки осуществить такое движение на практике не приводят к успеху — дело в том, что сколь угодно малая ошибка в задании скоростей ведет к значительным расхождениям траекторий в будущем. Эта неустойчивость, свойственная развитию любой достаточно сложной системы, не позволяет полностью предсказать ее поведение на длительный период времени (см. «Наука и жизнь» № 5, 2001 г.).
Математический анализ моделей сложных нелинейных открытых систем во второй половине ХХ века привел к возникновению новой науки — синергетики, открывшей общие принципы эволюции и механизмы их осуществления. В конце второго тысячелетия от Рождества Христова наука вновь вернула нас к древнему пониманию сущности мироздания — к представлению о двух силах, двух противоположных тенденциях, благодаря которым мир развивается и преображается, удерживаясь все же в относительном равновесии.
Сегодня на уровне математической теории можно утверждать, что любая достаточно сложная система, взаимодействующая со своим окружением, проходит в своем развитии определенные этапы. Вначале из неупорядоченных частей системы вдруг складываются и с колоссальной скоростью начинают расти множество структур — «новых форм». За счет противоположной, «разрушительной» тенденции скорость роста постепенно замедляется, некоторые формы исчезают, другие приобретают устойчивость. Эта тенденция рано или поздно одерживает верх, погружая все в изначальный хаос, и наступает кризис, порождающий структуры следующего этапа.
Таким образом, математическая модель развития совпадает с мифологической: согласно воззрениям Древней Индии, бог Брахма творит мир, упорядочивая хаос, а Шива разрушает его. В промежутках между двумя рождениями мир устойчив благодаря уравновешивающему началу — богу Вишну.

В античных мифах порождающее божество Дионис выхватывает из хаоса бессчетное множество форм, а гармонизирующее начало — Аполлон — уравновешивает его взрывную творческую энергию, успокаивает бешеный рост форм, придает миру соразмерность. Нарушение гармонии — конфликт, необходимый для развития, — погружает систему в животворящий хаос, дающий ростки новой жизни.
Хаос — неизбежный, обязательный атрибут жизни любой достаточно сложной системы. Геометрическим образом хаоса может служить запутанный клубок ниток: по такой же замысловатой, никогда не повторяющейся траектории движется система в период кризиса. Так ведет себя атмосфера Земли — хотя погода сегодня похожа на вчерашнюю, она всегда чем-то от нее отличается, и нет двух одинаковых дней. Так работают сердце и мозг — на их регулярные ритмы наложен хаотический фон, и его исчезновение ведет к скорой смерти пациента.
Этап кризиса характеризуется крайней неустойчивостью: малейшее движение в сторону от траектории может заставить систему сменить сценарий своего развития. Она может отправиться «на второй круг» своей эволюции, лишь немного отличающийся от предыдущего, а может ценой незначительного усилия перейти на принципиально иную, новую орбиту движения. Ведь, действительно, в клубке ниток рядом всегда есть нити, которые ведут в другом направлении, надо лишь «перескочить» на них — и наша судьба резко изменится.
В математических моделях выйти из кризиса можно за счет изменения так называемых внешних параметров — рано или поздно они изменят среду так, что в ней исчезнет неустойчивость, порождающая хаос, и клубок траекторий вытянется во множество почти параллельных нитей. Резкие изменения сценария развития на таких этапах спокойного развития практически невозможны — ведь все нити идут в одном направлении, и требуется долгое путешествие с нитки на нитку, чтобы существенно поменять направление движения.
Образом преодоления кризиса в мифологических концепциях служит ковчег — корабль, несущий семена новой жизни по бушующему морю во время потопа. Ковчег преодолевает хаос благодаря вере капитана, знающего, что потоп не вечен, имеющего ясную цель и осознающего свою ответственность за будущее. Универсальные математические сценарии развития тоже говорят о преходящем характере хаоса. И чтобы не застрять в бессмысленных метаниях, надо успокоиться, не упустить момент окончания кризиса, уловить нужную тенденцию и без лишних затрат выйти на устойчивую траекторию.
Сейчас предмет изучения науки — мир, для которого характерны кризисы и обвальные процессы, все чаще встречающиеся в нашей повседневной жизни; мир неустойчивостей, когда малые и локальные изменения влекут за собой глобальные последствия; мир, в котором идут процессы становления и возникновения порядка из хаоса; мир, в котором чередующиеся этапы предопределенности и непредсказуемости образуют причудливую череду событий, которые нас окружают и частью которых мы являемся.
Неустойчивые модели долгое время считались некорректными и «изгонялись» из науки. Отражением этого стала точка зрения Ж. Адамара, французского математика, сформулированная им в начале XX века. Вдохновленный успехами математической физики в точном описании явлений реального мира, он ввел понятие корректной задачи как задачи, для которой решение существует, единственно и устойчиво. Задачи, для которых не выполнено хотя бы одно из этих требований, он считал неинтересными для практики.
Однако жизнь показала, что неустойчивость — необходимый атрибут нашего мира. Тем интереснее точка зрения Анри Пуанкаре, соотечественника и современника Адамара. Роберт Гилмор, автор книги «Catastrophe Theory for Scientists and Engineers», пишет: «Основы современного подхода к определению качественных изменений в поведении решений обыкновенных дифференциальных уравнений были заложены почти 100 лет назад Пуанкаре… Эти работы… значительно опередили свое время. Сам Пуанкаре не смог реализовать намеченную им исследовательскую программу, так как был уже тяжело болен, а из его современников только А. Ляпунов следовал этой программе при изучении критических решений уравнений. После Ляпунова работы по теории бифуркаций практически прекратились… Такая ситуация сохранилась до 30-х годов, пока советские математики А. Андронов и Л. Понтрягин… вновь не обратились к идеям Пуанкаре. Особое оживление в этой области наблюдалось в 1950- 67 гг.»
Глобальность изменений во взглядах на мир и на его описание математическими моделями характеризует следующий исторический факт. В 60-х годах XX века сэр Джон Лайтхил, президент Международной ассоциации математических исследований, посчитал своим долгом принести извинение просвещенному сообществу за то, что в течение 300 лет математики вводили человечество в заблуждение, так как концепция абсолютного детерминизма оказалась далеко не безусловной.
Илья Пригожин, лауреат Нобелевской премии, создатель неравновесной термодинамики, утверждает: «Покуда мы требовали, чтобы все динамические системы подчинялись одним и тем же законам, хаос был препятствием к пониманию. В замкнутом мире классической рациональности поиск знания легко мог приводить к интеллектуальному снобизму и высокомерию. В открытом мире, который мы сейчас учимся описывать, теоретическое знание и практическая мудрость нуждаются друг в друге».
Теория нелинейных систем — математическая дисциплина, и сама по себе она не может ни предотвратить резкое ухудшение обстановки, ни обеспечить быстрый выход из застоя. Но, как любая теория, она позволяет глубже вникнуть в суть вещей, явлений и процессов реального мира. С точки зрения математики катастрофа и хаос — вовсе не обязательно крушение всех надежд или еще какая-нибудь беда. Это резкая перестройка системы, качественный скачок ее состояния: неожиданный поворот жизненного пути, социальная революция, экономический бум. И важно в преддверии этих кризисных ситуаций найти нужный путь, не дающий «застрять» в кризисе. Помогают в этом знаки судьбы — «флаги катастроф», предупреждающие умеющего их читать, что пришел подходящий момент для головокружительного прыжка вверх. А если упустить момент, то будут тянуться перед тобой глухие кривые окольные тропы…
Литература
- Арнольд В. Теория катастроф. — М.: Наука, 1990.
- Пригожин И. Конец определенности: Время, хаос и новые законы природы. — Ижевск: Редакция журнала «Регулярная и хаотическая динамика», 1999.
- Пригожин И., Стенгерс И. Время, хаос, квант: К решению парадокса времени. — М.: Прогресс, 1999.
- Стюарт И. Тайны катастроф. — М.: Мир, 1987.
С недавних пор термин «катастрофа» начал встречаться не только в газетных текстах, но и в той науке, которую принято считать самой абстрактной из всех,- в математике. Ну а то, какой степени абстракции достигла современная математика, можно продемонстрировать следующим примером: вместо высказывания «Петя вымыл руки» нынешние математики говорят весьма просто — существует такое t1<0, что образ точки t1 при отображении t—> Петя (t) принадлежит множеству грязноруких, и такое t2, что t1<t2<=0 и образ точки t2 при указанном выше отображении принадлежит дополнению к описанному множеству. Но если математики теперь изъясняются на столь эзотерическом языке, то какой смысл они вкладывают в понятие катастрофы? О том, что такое математическая теория катастроф, рассказывает одни из крупнейших математиков современности, член-корреспондент Академии наук СССР Владимир Игоревич АРНОЛЬД.
Сначала мысль, воплощена
В поэму сжатую поэта,
Как дева юная, темна
Для невнимательного света;
Потом, осмелившись, она
Уже увёртлива, речиста,
Со всех сторон своих видна.
Как искушённая жена
В свободной прозе романиста;
Болтунья старая, затем
Она, подъемля крик начальный.
Плодит в полемике журнальной
Давно уж ведомое всем.
Е. Баратынский
Первые сведения о теории катастроф появились в начале 70-х годов. В массовых журналах типа «Тайм» и «Ньюсуик» сообщалось о перевороте в математике, сравнимом разве что с изобретением Ньютоном интегрального и дифференциального исчисления. Журналисты вдохновенно писали, что новая наука — теория катастроф — для человечества гораздо ценнее, чем классический математический анализ: в то время как ньютоновская теория позволяет исследовать лишь плавные, непрерывные процессы, теория катастроф даёт универсальный рецепт для исследования всех скачкообразных переходов, разрывов и внезапных качественных изменений. Появились сотни научных и околонаучных публикаций, в которых теория катастроф применялась, например, к эмбриологии, кардиологии, психологии, лингвистике, экономике, социологии и геологии, не говоря уже о таких «естественных» дисциплинах, как оптика, теория устойчивости упругих конструкций и кораблей при волнении или, например, теория элементарных частиц. Среди публикаций по теории катастроф есть самые экзотические, в частности о психических расстройствах и восстаниях заключённых, о поведении биржевых игроков и влиянии алкоголя на водителей и даже о цензуре на эротическую литературу.
Маяковский заметил как-то, что сущность математики не в том, какие предметы она исследует, а в том, какие законы обнаруживает. Человек, открывший, что дважды два четыре, говорил он, был великим математиком, даже если он открыл это, считая окурки. Тот, кто теперь считает по той же формуле паровозы,- вообще не математик.
В прошлом веке математику делили на чистую — равно применимую к окуркам и паровозам — и прикладную, то есть специально приспособленную к паровозам. А сравнительно недавно, когда потребовалось перейти от паровозов к атомам, самолётам и спутникам, вдруг оказалось, что чистая — «окурочная» — математика с её необычными объектами, такими, как представления групп, комплексные многообразия, многомерные пространства, и довольно-таки отвлечёнными разделами вроде топологии или функционального анализа гораздо лучше приспособлена к новым задачам, чем созданная для чисто практических нужд «паровозная».
А какова же по этой классификации теория катастроф, к чему она ближе, к чистой математике или прикладной?
Рис. 1. В законе «Достижения пропорциональны усилиям» отражается фундаментальный принцип математического анализа: всякая гладкая функция в малом (то есть при малых приращениях аргумента) приближённо линейна.
Оказывается, что математическим источником теории катастроф служит сравнительно молодой раздел чистой, «настоящей» математики, который называется теорией особенностей гладких отображений. Фактически теория особенностей — смелое обобщение исследования функций на максимумы и минимумы. Почему такое исследование необходимо? Дело в том, что минимумы и максимумы представляют собой критические точки функции, которые во многом определяют её поведение. Известный французский математик Поль Монтель выразил это так: «Функции, как и живые существа, характеризуются своими особенностями». А чтобы понять, как именно, нам придётся рассмотреть несколько типичных примеров.
Современник Ньютона, английский учёный Гук, установил следующий закон, справедливый для упругих тел: удлинение такого тела, например, обычной пружины, почти пропорционально приложенной силе, пока она мала. (Это утверждение впоследствии так и назвали — законом Гука.) Точно так же в нормальных рыночных экономических условиях приращение спроса пропорционально малому уменьшению цены. И вообще очень часто достигаемый эффект оказывается пропорциональным затраченным усилиям. Однако нужно иметь в виду, что это верно лишь при малых приращениях, как часто говорят, локально (скажем, нынешнее уменьшение потребления алкоголя вряд ли пропорционально повышению цены на водку).
Приведённые примеры отражают один из универсальных законов:
I. В окрестности некритической точки приращение функции почти пропорционально приращению аргумента.
Фактически этот закон отражает основной принцип классического математического анализа — всякая гладкая, то есть не имеющая изломов и «клювиков», функция на малых участках (как говорят, в малом) приближённо линейна. Иными словами, гладкую кривую можно заменить её касательной (рис. 1). С простейшими универсальными законами такого рода мы встречаемся столь часто, что уже перестали им удивляться. Но как прийти к пониманию этих законов, «прочувствовать» их? Так вот, оказывается, что исследование зависимости всевозможных математических объектов от определяющих их параметров и приводит к универсальным законам. Именно в этом, по существу, основной вывод математической теории особенностей.
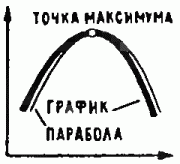
Рис. 2. Универсальный закон квадратичности: в окрестности точек максимума или минимума приращения функции (соответственно отрицательное или положительное) приблизительно пропорционально квадрату приращения аргумента. Вдобавок типичная кривая переходит в точке касания с одной стороны аппроксимирующей её параболы на другую.
Если рассматривать функцию не локально, то есть не на малом участке, а в целом, то она может быть и сильно нелинейной, например, иметь максимумы и минимумы. В окрестности точки максимума или минимума график типичной функции можно приближённо заменить параболой (рис. 2). Отсюда следует универсальный закон:
II. В окрестности максимума (минимума) приращение типичной функции почти пропорционально квадрату приращения аргумента.
В частности, небольшое отклонение аргумента от его оптимального значения практически не сказывается на значении функции. Например, малый поворот двигателей реактивного самолёта (рис. 3) практически не меняет результирующую силу тяги, но спасает от реактивной струи хвостовое оперение. Действительно, потеря тяги пропорциональна квадрату малого угла поворота, то есть оказывается, как принято говорить, величиной более высокого порядка малости по сравнению с отклонением струи, которое пропорционально величине самого угла. Другой пример: с приближением к оптимальному состоянию затрачиваемые усилия перестают сказываться на достижениях.
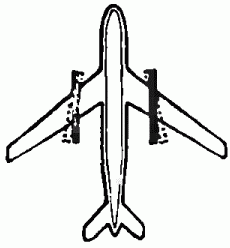
Рис. 3. Как спасти хвостовое оперение реактивного самолёта от струи раскалённых газов? Небольшое отклонение значения аргумента от оптимального практически не сказывается на значении функции. В частности, малый поворот реактивных двигателей не меняет результирующую силу тяги.
Третий универсальный закон можно сформулировать так:
III. Типичная плоская кривая касается прямой не более, чем в двух точках.
Действительно, от касания в трёх точках можно избавиться малым изменением формы кривой (рис. 4), касание же в двух точках устойчиво, то есть не исчезает при малом шевелении кривой. Правда, чтобы сохранить касания в двух точках, придётся пошевелить и саму касательную. Третий универсальный закон имеет фундаментальное значение в теории оптимизации (см. рис. 5).

Рис. 4. Типичная кривая не имеет тройных касательных. При этом касание в двух точках устойчиво» то есть не исчезает при малом шевелении кривой.
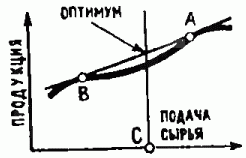
Рис. 5. Выбор пульсирующего оптимального режима. Предположим, что зависимость скорости выпуска продукции каким-либо производством (например, мельницей) от скорости подачи сырья изображается невыпуклой кривой. Как организовать работу, чтобы суммарный выход продукции при заданной средней скорости С подачи сырья (то есть при заданном расходе сырья за большое время) был максимальным?
Универсальные законы, которым подчиняются более сложные системы (описываемые многими функциями многих переменных), уже не столь очевидны. Вот один из примеров:
IV. Типичная поверхность не касается никакой прямой более чем в четырёх точках.
В этом можно убедиться после некоторого экспериментирования с картофелинами и карандашом. Эксперимент показывает также, что касание в 4 точках устойчиво.
Во всех рассмотренных ситуациях речь идёт об универсальных законах, которые выполняются для любых гладких объектов (функций, кривых, поверхностей), за исключением лишь некоторых специальных, «нетипичных». Интересно, что такие, казалось бы, простые объекты, как плоскость и цилиндр,- нетипичные поверхности.
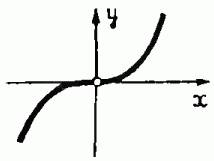
Рис. 6. График функции у=х3. Эта функция имеет при х=0 нетипичную, кубическую особенность.
Теперь мы, пожалуй, уже готовы к тому, чтобы понять, что имеют в виду математики, произнося слово «катастрофа». Правда, вначале нам придётся сделать ещё одно небольшое математическое усилие. Представим себе кубическую зависимость — функцию у = х3 (рис. 6). В нуле она имеет «нетипичную» кубическую особенность. Но если задана не индивидуальная функция, а целое семейство функций, зависящих ещё от некоторого параметра, то оказывается, что существует такое значение параметра, при котором кубическая особенность становится устойчивой. Слово «устойчивость» здесь означает, что во всяком близком семействе при некотором близком значении параметра встретится точно такая же особенность.
Универсальный пример такого семейства- множество кубических функций у = х3+рх переменной х, зависящих к тому же от параметра р. Вид графика таких функций при разных значениях параметра показан на рис. 7.
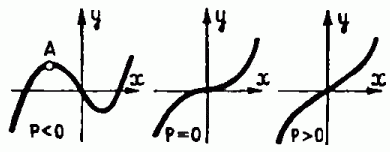
Рис. 7. Универсальная деформация кубической особенности. При возрастании параметра максимум и минимум функции сближаются и в конце концов исчезают, «убив» друг друга.
Пока параметр р отрицателен, функция имеет вблизи нуля локальные максимум и минимум. Когда параметр р стремится к нулю, максимум и минимум сближаются, и при нулевом значении параметра возникает кубическая особенность. При положительных значениях параметра и максимум, и минимум исчезают, «убив» друг друга. Все эти явления универсальны и устойчивы, они наблюдаются и в семействах, близких к рассматриваемому. Поэтому такие явления имеют широкую область применимости.
Пусть, например, наша функция характеризует состояние экономики (скажем, величину дохода правящего класса) в зависимости от какого-либо параметра. (В качестве такого параметра можно взять, к примеру, предприимчивость населения или гласность принятия решений, или правдивость печати.) Если экономика регулируется так, чтобы обеспечивать максимизацию функции, то система будет находиться в точке максимума. А до тех пор, пока с изменением дополнительного параметра этот максимум — локальный оптимум — не исчезнет.
В этот момент система будет вынуждена скачком перейти в далёкое от исходного состояние В (рис. 8). Такого рода перескоки и получили название катастроф, так как они связаны с резкими изменениями в состоянии системы и могут приводить к её разрушению.
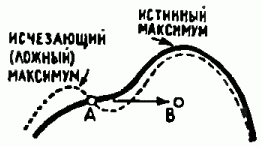
Рис. 8. Катастрофическое изменение режима. Модели, основанные на представлениях теории катастроф» некоторые авторы пробуют применять и социальным системам и экономке.
Если бы мы не ограничивались узкими рамками малых изменений вблизи рассматриваемого локального оптимума, то картина могла бы быть, например, такой. Вначале оптимальное решение единственно (А на рис. 9). По мере развития системы возникает побочный максимум В — новый локально-оптимальный, но вообще-то не наилучший режим. Он рождается вместе с близким локальным минимумом. Кстати, это явление рождения двух экстремумов описывается таким же универсальным законом, как и изображённое на рис. 7 их взаимное уничтожение, меняется только направление изменения параметра. Далее, побочный максимум обгоняет исходный (С). Начиная с этого момента, новый режим уже выгоднее старого. Но переход на него затруднён необходимостью резкого перескока — катастрофы. Отсюда вытекает правило:
V. При плавном переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.
Оказывается, оптимальный режим — пульсирующий: он составляется из чередующихся периодов интенсивной загрузки сырья (точка А) и слабой загрузки (точка В). Действительно, требуется так распределить массы по кривой, изображённой на рисунке, чтобы центр тяжести лежал над точкой С и находился возможно выше. Такое распределение масс сосредоточено в двух точках А и В касания кривой с прямой.
Оптимальный режим составляется из смеси двух, а не большего числа режимов, именно потому, что прямая касается типичной кривой не более чем в двух точках (см. рис. 4).
В линейных системах малое изменение параметра в сторону лучшего режима улучшает положение. В отличие от этого, после достижения локального оптимума малые изменения управляющего параметра, направленные в сторону лучшего режима, не улучшают, а ухудшают положение. И если, как это обычно бывает, система сама стремится локально оптимизировать своё состояние, то она будет отвечать на недостаточно радикальные изменения возникновением сильных тенденций возврата к старому режиму. Этим, думается, можно объяснить неудачу многих реформ, в частности экономических.
В живой природе аналогичная трудность, например, необходимость полной перестройки организма гусеницы для образования бабочки преодолевается при помощи специальной стадии — куколки. В этом случае отжившая система (гусеница) сама создаёт в своих недрах новую систему, которая впоследствии уничтожает старую (куколка в конце питается остатками гусеницы).
Наконец, в ходе дальнейшего развития системы исходное локально-оптимальное состояние вообще исчезает (D) и переход на далёкий от первоначального режим становится неизбежным (Е).
Универсальный закон (рис. 7) приводит к выводу:
VI. Расстояние от исчезающего локально-оптимального режима до движущегося ему навстречу локально-минимального — порядка квадратного корня из отличия параметра от катастрофического значения.
Поэтому в момент катастрофы оба режима сближаются с бесконечной скоростью. Это, кстати, объясняет, почему так трудно бороться с грозящей катастрофой, когда её признаки сделались уже заметными.
Описанный сценарий оказывается лишь одной из возможных последовательностей локальных метаморфоз, качественных перестроек, или, как выражаются математики, бифуркаций. Все возможные сценарии взаимодействия двух локально-оптимальных режимов даются, как выяснилось, универсальным законом
у = х4 + ах2 + bх
с параметрами a и b. На рис. 10 изображён график экстремального значения у как функции параметров a и b.

Рис. 9. Сценарий глобальных перестроек в развивающейся системе. При плановом переходе от одного локально-оптимального режима к другому необходимо временное ухудшение.
Сценарий, описанный выше, изображается на этом графике путём I, заканчивающимся катастрофическим скачком. Однако к той же самой конечной цели можно прийти без катастрофы, даже зайдя уже достаточно далеко по катастрофическому пути. Для этого надо вернуться назад и обойти разделяющую конкурирующие режимы точку с другой стороны (путь II).
Поверхность, изображённая на рис. 10, называется «ласточкиным хвостом». Она постоянно встречается в теории особенностей в качестве универсальной модели. Например, такие же «ласточкины хвосты» имеют фронты типичных воли, распространяющихся в трёхмерном пространстве. В местах особенностей волны особенно сильны. Именно этими особенностями объясняются, в частности, радуга на небе и разрушительная ударная волна от сверхзвукового самолёта.
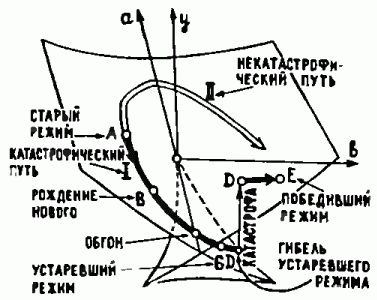
Рис. 10. Ласточкин хвост: универсальный закон зависимости оптимальных значений от параметров.
Универсальных законов, подобных приведённым выше, оказалось не так уж много (хотя число их, конечно, растёт с увеличением числа переменных и параметров). Кроме ласточкиного хвоста в трёхмерном пространстве, особенно часто встречается ещё зонтик Уитни-Кэли (рис. 11) — поверхность, заданная уравнением у2 = zx2. Зонтиком эта поверхность называется потому, что, кроме нарисованной на рис. 11 поверхности, выписанному уравнению удовлетворяет и отрицательная часть оси z — своего рода «ручка» зонтика.
Если объекты нашего исследования характеризуются двумя параметрами, а мы, не зная их, измеряем три характеристики объекта и изображаем результат измерений точкой трёхмерного пространства, то полученные точки расположатся на некоторой поверхности. И вот оказывается, что, несмотря на полную гладкость зависимости измеряемых характеристик от параметров объекта, получающаяся поверхность, вообще говоря, имеет особенности, а именно зонтики, локально устроенные так, как указано на рис. 11.
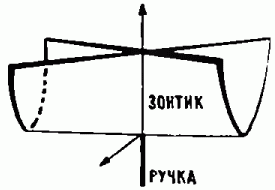
Рис. 11. Зонтик Уитни — Кэли. Зонтиком эта поверхность называется потому, что уравнению, задающему поверхность, удовлетворяет и отрицательная часть оси Z — своего рода «ручка» зонтика.
Характерная особенность образуется при проектировании гладкой поверхности общего положения на плоскость.
Если соединить графики функций рис. 7 в одну поверхность (рис. 12) и спроектировать эту поверхность на плоскость (p, y) вдоль оси х, то видимый контур поверхности будет иметь остриё (точки возврата). На самой поверхности в этом месте нет никакой особенности. Особенность имеет лишь проектирование. При изменении направления проектирования особенность перемещается по поверхности. Эта особенность называется «сборкой Уитни».
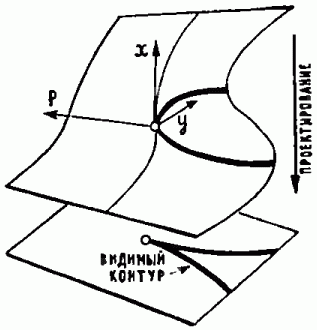
Рис. 12. Сборка Уитни: универсальный закон, в соответствии с которым изменяется внутреннее состояние системы в зависимости от параметров.
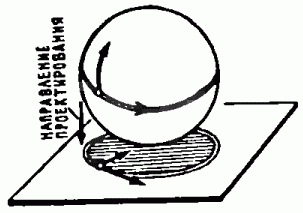
Рис. 13. Особенность, называемая складкой, возникает, в частности, при проектировании сферы на плоскость в точках экватора.
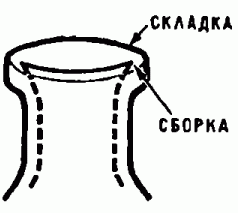
Рис. 14. Экспериментальное наблюдение сборки Уитни. На поверхности бутылки можно увидеть две сборки. Они устойчивы, в чём можно убедиться, покачивал бутылку.
В 1955 году американский математик Хасслер Уитни опубликовал работу «Об отображениях плоскости на плоскость». Фактически именно эта работа и заложила основу теории особенностей гладких отображений, а с нею и теории катастроф. Отображение поверхности на плоскость — это сопоставление каждой точке поверхности точки плоскости. Уитни заметил, что в случаях «общего положения», то есть во всех случаях, кроме некоторых исключительных, встречаются особенности лишь двух видов — все другие разрушаются при малом «шевелении» тел или направлений проектирования, тогда как эти два вида особенностей устойчивы и сохраняются при малых деформациях отображения.
Сборка — одна из таких особенностей, вторую особенность Уитни назвал складкой, она возникает, если проектировать сферу на плоскость в точках экватора (рис. 13). Две сборки можно увидеть на поверхности бутылки (предпочтительнее из-под молока, рис. 14). Покачивая бутылку, мы экспериментально убеждаемся в том, что сборка устойчива. И вообще, отображения гладких поверхностей на плоскость окружают нас со всех сторон. Действительно, большинство окружающих нас тел ограничено гладкими поверхностями, при этом видимые контуры тел — проекции поверхностей, ограничивающих тела, на сетчатку глаза. Приглядываясь к окружающим нас телам, например, к лицам людей, мы можем изучить особенности видимых контуров. Например, точки сборки можно увидеть в чертах окружающих нас лиц там, где линия контура «исчезает» (рис. 15). Если применительно к человеческим лицам говорить на геометрическом языке, то можно заметить, что линия контура имеет касательную вплоть до точки сборки, но с приближением к этой точке кривизна линии растёт до бесконечности.
Теорема Уитни стала прообразом многочисленных универсальных законов строения особенностей, открытых в последующие годы. Простейшие из этих законов были уже известны в конкретных примерах специалистам в соответствующих областях. Историки науки недавно подметили, что до появления теории особенностей открытия этого рода особенно часто встречались в работах, удостоенных Нобелевской премии. Положение здесь такое же, как с математическим анализом: Гюйгенс решал без его помощи практически все задачи, решаемые Ньютоном и Лейбницем с помощью анализа, но для этого нужно было иметь гений Гюйгенса. Теперь же такие задачи благодаря анализу легко решает любой студент. Точно так же теория особенностей сделала легкодоступным тонкое искусство построения правильных моделей явлений, когда отбрасываются большие, но «физически несущественные» величины и сохраняются меньшие, но «физически важные» члены.

Рис. 15. Складки и сборки на лице Мики Морозова (портрет Валентина Серова).
Из предшественников теории особенностей упомяну Гюйгенса (теория эволют и эвольвент), Гамильтона (теория систем лучей), Кэли (зонтики, фронты и каустики), Пуанкаре (теория бифуркаций, включая — катастрофисты обычно этого не знают — построение «версальных деформаций»), А. А. Андронова (структурная устойчивость, бифуркации аттракторов), Максвелла (фазовые переходы), Гиббса (правило фаз), Н. Н. Семёнова (тепловой взрыв), Я. Б. Зельдовича (теория горения и космология), Пирси (волновая оптика), Койтера (теория упругости), Л. Д. Ландау (фазовые переходы второго рода) и т. д.
Понимание того, что в основе всех этих (и многих других) исследований лежит одна и та же математическая структура, пришло не сразу, но когда это было осознано, то прогресс в каждой из перечисленных областей начал немедленно приводить к продвижениям во всех остальных. В настоящее время теория особенностей, бифуркаций и катастроф — один из наиболее бурно развивающихся отделов математики.
Термин «катастрофа» был введён в конце 60-х годов французским математиком Р. Томом для обозначения качественного изменения объекта при плавном изменении параметров, от которых объект зависит. Этот термин, призванный заменить использовавшиеся до него термины «бифуркация», «перестройка», «метаморфоза», завоевал широкую известность после того, как в начале 70-х годов английский тополог К. Зиман предложил употребить название «теория катастроф» для соединения теории особенностей, теории бифуркаций и их приложений.
Математику трудно согласиться с тем, что введение нового термина, не сопровождаемое открытием новых фактов, представляет собой значительное достижение. Однако успех «кибернетики», «странных аттракторов», «синергетики» и «теории катастроф» показывает плодотворность словотворчества как метода научной работы. Этот метод, впрочем, известен давно, и Пуанкаре употреблял его уже вполне сознательно.
«Трудно поверить,- говорил он,- какую огромную экономию мысли может осуществить одно хорошо подобранное слово. Часто достаточно изобрести одно новое слово, н это слово становится творцом». Более того, согласно Пуанкаре «математика-это искусство давать одно и то же название различным вещам». «Факт… приобретает своё значение лишь с того дня, когда более проницательный мыслитель подметит сходство, которое он извлечёт на свет и символически обозначит тем или иным термином» (все 4 фразы — из «Науки и метода», глава «Будущее математики», стр. 296-301 в книге А. Пуанкаре «О науке», М., 1983). Однако Ньютон, сравнивая математику с теорией типа теории катастроф, писал: «Математики, которые всё открывают и устанавливают и проделывают всю работу, должны довольствоваться ролью сухих вычислителей и чернорабочих. Другой (катастрофист.- В. А.), который всего лишь все схватывает и на всё претендует, присваивает себе всё изобретения как своих последователей, так и предшественников».
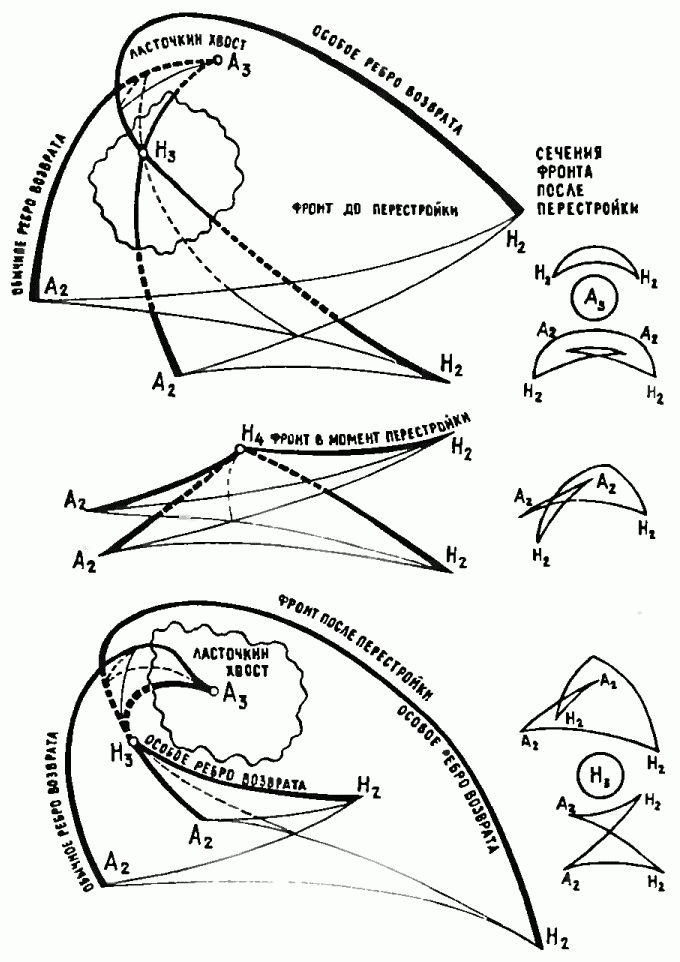
Рис. 16. Метаморфоза Н4 на волновом фронте.
При распространении воли первоначально гладкий волновой фронт перестраивается и приобретает сложные особенности. Здесь изображена одна из типичных метаморфоз уже особого волнового фронта, огибающего гладкое препятствие в трёхмерном пространстве. Такая перестройка волнового фронта возникает в некотором отдалении от поверхности препятствия. Исследование этой метаморфозы волнового фронта основано на геометрии правильного 600-гранника в четырёхмерном пространстве. Более простая особенность, обозначенная на рисунке Н3, соответствует обычному икосаэдру (правильному двадцатиграннику в трёхмерном пространстве), особое ребро возврата Н2 правильному пятиугольнику на плоскости.
При практическом применении теории особенностей и теории катастроф мы встречаемся с такими же трудностями, которыми всегда сопровождаются применения математики. Нет сомнения, что арифметика полезна: умножать и складывать лучше, чем отнимать и делить. Однако даже самое безупречное умножение чисел само по себе ещё недостаточно. (С аналогичной трудностью столкнулся Буратиио, когда решал предложенную ему Мальвиной арифметическую задачу. Затруднение вызвала не арифметика, а более важная проблема: «Зачем я отдал некту два яблока?!»)
Таблица умножения полезна для бухгалтерского учёта, но не предохраняет от хищений социалистической собственности. Точно так же знание универсальных законов, по которым происходят катастрофы, само по себе ещё не предохраняет от них. И без теории ясно, что несоблюдение техники безопасности, а также падение уровня компетентности специалистов неизбежно повышает вероятность катастроф. Там, где разорвана обратная связь в системе управления, где ответственные решения принимаются лицами или организациями, не несущими материальной ответственности за их последствия («стрелочник виноват»), катастрофы становятся неизбежными, что и наблюдается, к сожалению.
«Шахта становится слишком глубока,- писал о математике в 1781 году Лагранж Даламберу,- и, если не будут найдены новые жилы, придётся совсем её забросить,., иначе места по математике в Академии станут тем, чем уже стали кафедры арабского языка в университете».
Сомнения в полезности математики высказывал и Маяковский («Гимн учёному»):
…И ему не нудно,
что растёт человек глуп и покорен.
Ведь зато он может
ежесекундно
извлекать квадратный корень.
В такой репутации своей науки отчасти виноваты сами математики, «складывающие простые числа, вместо того, чтобы их умножать», как говорил Л. Д. Ландау.
Правда, последнее десятилетие знаменуется крутым поворотом современной математической науки от абстрактно — аксноматических исследований к естествознанию (это проявилось даже в тематике такого форума абстрактной математики, как знаменитый семинар Бурбаки). Теория особенностей — одна из тех жил, о которых говорил Лагранж, и одна из самых живых ветвей современной математики, где её наиболее абстрактные отделы (алгебраическая геометрия, теория групп отражений, теория алгебр Ли) соединяются с самими прикладными (теория динамических систем, геометрическая и физическая оптика, оптимизация и теория управления).
На рис. 16 изображена одна из типичных и устойчивых метаморфоз распространяющегося волнового фронта в задаче об обходе препятствия в трёхмерном пространстве (этот результат был получен в 1984 году советским математиком О. П. Щербаком). Задача относится к теории оптимального управления, решение же её оказывается связанным (довольно таинственным образом) с «калейдоскопом Н4» — правильным 600-гранником в четырёхмерном пространстве. И именно теория таких многогранников (давно построенная в «абстрактной» математике) позволила разобраться в сложных перестройках фронта, изображённых на рис. 16.
В подобных неожиданных проявлениях загадочного единства всего сущего — особая притягательность теории особенностей, да и вообще математики. Как сказал поэт:
Мир создан купно. Целостность его
Не устаёт показывать планета.
И вот в глаза бросается родство
То тут, то там сияющего света.
Наверно, есть какое-то ядро,
Откуда свет расходится повсюду:
И в зрелый цвет сентябрьских щедрот,
И в нашей жизни трепетное чудо…
Член-корреспондент АН СССР В. АРНОЛЬД.
ЛИТЕРАТУРА
Арнольд В. И. Теория катастроф. М.: МГУ. 1983.
Гилмор Р. Прикладная теория катастроф. М.. «Мир». 1984.
Постон Т., Стюарт Я. Теория катастроф и её приложения. М.. «Мир», 1980.
Томпсон Дж. М. Т. Неустойчивости и катастрофы в науке и технике. М «Мир», 1985
Машина катастроф
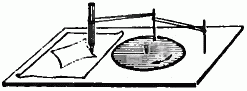
Это нехитрое устройство каждый может изготовить сам. Нужно взять дощечку и, вырезав из картона диск, прикрепить его иглой в центре к доске так, чтобы диск мог свободно вращаться. Другая игла втыкается только в диск на его краю, а третья-только в доску. Чтобы закончить сборку машины, нужны ещё две ленты из легко растяжимой резины (можно взять аптекарские резинки), карандаш и лист бумаги.
После того, как игла на краю диска соединена с неподвижной иглой и карандашом резинками, мы ставим острие карандаша в некоторой точке на листе бумаги и тем самым натягиваем резинки. Диск при этом устанавливается в некотором положении. Теперь при движении карандаша по листу бумаги диск будет поворачиваться, и оказывается, что при некоторых положениях карандашного острия малое изменение его положения способно вызвать «катастрофу», то есть скачкообразный поворот диска. Если на листе бумаги отметить места всех таких катастроф, то получится «кривая катастроф». Оказывается также, что полученная «кривая катастроф» сама имеет четыре точки возврата. Интересно, что при пересечении «кривой катастроф» скачок может происходить, а может и не происходить в зависимости от того, по какому пути карандаш обходил точки возврата. Экспериментируя с машиной катастроф и анализируя её поведение (движение, как говорят физики и математики, изображающей точки по поверхности равновесия), можно предметно убедиться в том, как теория особенностей предсказывает геометрию катастроф — перескоков из одного равновесного состояния в другое.
Сергей Мелихов, Школа Свободных Наук
ЧТО ТАКОЕ ТЕОРИЯ КАТАСТРОФ?
Утром, прежде чем сделать последний глоток чая, загляните в свою чашку. Если за окном солнечно, и свет в помещении достаточно яркий, вы обязательно увидите на дне чашки характерную световую линию. Напоминает опрокинутую цифру «три». Или яблоко. Или… ну, в общем, не важно, что напоминает (Рис. 1).

Эта линия (а говоря математическим языком – «кривая») называется каустика. Стоит обратить внимание на неё один раз, и она начнёт преследовать вас повсюду. Например, в кастрюле или в ведре с водой (Рис. 2).

В переводе с греческого «каустикос» означает «жгучий». Как возникает это явление и почему так называется?
Допустим, источник света – это ваше окно. Тогда свет – это пучок параллельных лучей. Каждый луч отражается от стенки чашки по закону геометрической оптики – «Угол падения равен углу отражения» (Рис. 3).
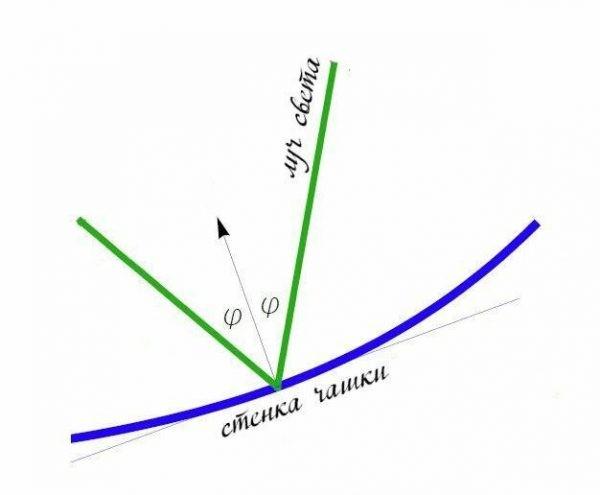
Каждый следующий луч отражается от стенки чашки под немного другим углом (ведь эта стенка искривлённая). Отражённые от стенки лучи пересекаются строго определённым образом. Из точек их пересечения и образуется каустика! Более светлая, потому что свет в точках пересечения лучей концентрированный! (Рис. 4)
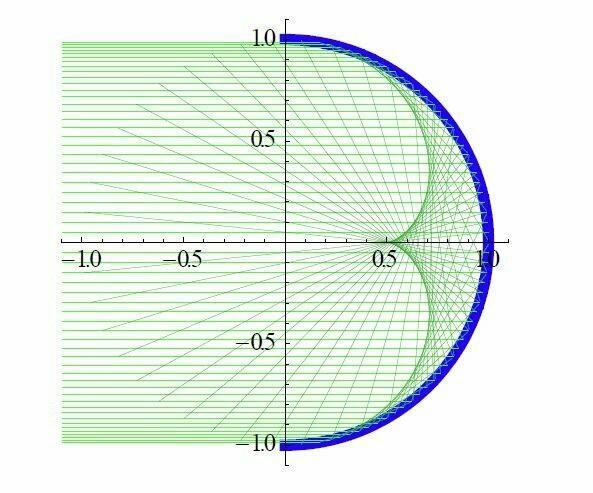
Именно за каустиками мы наблюдаем, когда любуемся игрой света на на борту корабля или на дне бассейна (Рис. 5).

Каустики изучает один из самых молодых разделов математики, у котоого очень интригующее название – «теория катастроф». Что это такое?
Есть старинная восточная притча. Жил да был жадный торговец. Поехал он на базар купить соломы и взял с собой одного-единственного верблюда. Купил – и давай грузить тюки с соломой верблюду на спину! Грузит, грузит, и всё ему мало. «Смотри, – говорят ему, – как бы верблюд твой не умер от такой тяжести, имей совесть!» – «Ничего, – отвечает жадина, – выдержит!» И продолжает грузить. Верблюд уже еле-еле на ногах стоит, а купец только руки потирает, подсчитывает будущие барыши. Наконец, тронулся верблюд с места, а жадина не выдержал: «Ну ещё чуть-чуть!» – и положил на спину верблюду всего-то одну соломинку. Ноги у верблюда подкосились, он упал и умер. Остался купец ни с чем – не на себе же ему солому везти? А с тех пор люди стали говорить: «Одна соломинка может сломать спину верблюду».

Волк — не верблюд, но процесс тот же самый.
Обычная математика любит изучать такие процессы, которые принято называть «непрерывными», «гладкими». Это означает, что маленькие изменения управляющих параметров приводят к таким же маленьким изменениям итоговых характеристик. Переводим на русский. Если нажать на педаль газа в автомобиле несильно, совсем чуть-чуть, то автомобиль ускорится тоже совсем немножечко.
- Движущийся автомобиль – это система.
- Педаль – это управляющий параметр.
- Нажатие педали – изменение управляющего параметра.
- Ускорение автомобиля – итоговая характеристика.
Теория катастроф же изучает совершенно другое – так называемые «особые точки», то есть точки, в которых самые малые изменения входных параметров приводят к резкому и безвозвратному изменению характеристик всей системы. Нажимаешь на педаль «ещё чуть-чуть», а автомобиль взлетает…
Возьмём, например, нашу историю про купца и верблюда. С точки зрения математики, в этой сказке есть одна система (верблюд + груз соломы), есть управляющий параметр (вес соломы, то есть количество соломинок, уложенных верблюду на спину) и есть итоговая характеристика (довезёт верблюд груз или нет).
Допустим, мы начинаем добавлять по одной соломинке (ведь одна соломинка практически ничего не весит, правда?). Тысяча соломинок, десять тысяч, двадцать… Верблюду всё тяжелее, но он стоит на ногах, он способен идти, хоть и медленно… И вдруг в какой-то момент мы добавляем всего лишь ещё одну соломинку – и верблюд падает замертво! Характеристики нашей системы кардинально изменились! И даже если мы начнём разгружать беднягу-верблюда, – ни ему, ни нам это не поможет. Вернуть всё назад уже не выйдет! Вот эта самая «точка невозврата», «точка последней соломинки» и называется в математике вырожденной особой точкой или «точкой катастрофы».
ТОЧКА КАТАСТРОФЫ
В природе существует множество процессов, которые можно рассматривать как математические катастрофы. Возьмите старую резинку для волос. Она сделана из упругого материала, который (согласно школьной физике) подчиняется простому закону (закону Гука): чем больше мы удлиняем резинку, тем сильнее она нам «сопротивляется», стремится вернуть себе исходную форму. Но что произойдёт, если мы – пускай даже очень медленно и осторожно! – станем удлинять её всё дальше и дальше?
В определённый момент её структура изменится, её упругие характеристики исчезнут – и даже если мы отпустим её, исходную форму она уже не примет, а просто повиснет на руках. Всё, резинка испорчена, «растянулась». Ну а если мы потянем её ещё дальше – она и вовсе разорвётся, правильно? Перед нами снова математическая катастрофа: совсем небольшое дополнительное усилие (растягивание резинки) в какой-то момент резко и необратимо меняет свойства объекта.
Само собой, математическая катастрофа может стать причиной самой настоящей катастрофы. Представьте себе летящий самолёт. Его крыло создаёт подъемную силу, которая не даёт самолёту упасть. Однако эта подъемная сила зависит от скорости самолёта. Если пилот начнёт сбрасывать скорость, лететь всё медленнее и медленнее, то в какой-то момент (вот она, «точка катастрофы»!) подъемная сила вдруг резко уменьшится – и самолёт внезапно теряет управляемость, «сваливается в штопор», начинает бесконтрольно падать и в итоге разбивается об землю. Хорошо, если пилот успеет выпрыгнуть с парашютом! Обратите внимание: если самолёт «сваливается», то увеличение скорости само по себе не сможет вернуть ему управляемость, просто так «отыграть назад» у пилота не выйдет.
БИФУРКАЦИЯ
Поведение исследуемой системы вблизи точки катастрофы математики часто называют «бифуркацией», то есть «двойной вилкой». Допустим, если наш самолёт летит на предельно малой скорости («скорости сваливания»), в каждый момент у нас образуется «вилка» – он с равной вероятностью (как любят говорить, «пятьдесят на пятьдесят») может или продолжать полёт, или потерять управляемость и свалиться в штопор. В точности такая же бифуркация присутствует и в опыте с резинкой («растянется – не растянется»), и в сказке про верблюда («выдержит – не выдержит»).
КАТАСТРОФЫ СОЦИАЛЬНЫЕ И ПСИХОЛОГИЧЕСКИЕ
Где ещё можно использовать методы теории катастроф? Ну, например, при исследовании поведения животных и даже нас, людей. Как это выглядит? Вообразите ситуацию: учительница ведёт в парк на экскурсию первоклассников. Первоклассники, как водится, ведут себя не очень примерно – то один отбежит в сторону, то другой начнёт задираться, то третий дёрнет девочку за косичку… Учительница сдержанно, с улыбкой пытается наладить дисциплину: «Петров, прекрати… Сидоров, вернись в строй… Алёша, возьми за руку товарища и не хулигань». Так продолжается пять минут, десять… И вдруг в какой-то момент (вот она, «критическая точка», «точка катастрофы», узнали?) учительница срывается на крик: «А ну все встали на места! Все замолчали!» Дети тут же притихают и обиженно шепчут – «А что случилось? Да мы же ничего такого не делали…»
Непедагогично, но ведь знакомо, правда? Довели бедную Мариванну до белого каления, негодники. А ведь такие ситуации могут возникать и среди взрослых, и не только в школе – но и на производстве, в армии, в научной экспедиции, и результаты могут быть очень неприятными.
КАТАСТРОФЫ МАТЕМАТИЧЕСКИЕ
Давайте проверим, насколько хорошо мы поняли, какая разница между математическими и «настоящими» катастрофами.
Скажем, падает на Землю из космоса метеорит – и взрывается. Катастрофа? Ещё какая, спросите у динозавров. Однако является ли это явление математической катастрофой? Нет. Когда метеорит врезался в землю, его скорость (управляющий параметр) падает резко, скачком – и состояние его соответственно меняется скачком (происходит взрыв). Назвать это «катастрофой» в математическом смысле будет некорректно.
А теперь рассмотрим выражение «последняя капля» (та самая последняя капля, которая «переполняет чашу терпения»). Возьмём стакан и наполним его до краёв водой. А потом возьмём пипетку и будем добавлять в полный стакан по капельке… В конце концов вода разольётся, причём на стол прольётся не одна капля воды, а больше!
С обыкновенной точки зрения эта ситуация катастрофой не является – а вот с точки зрения математики перед нами типичная математическая катастрофа.







Оставить комментарий